|
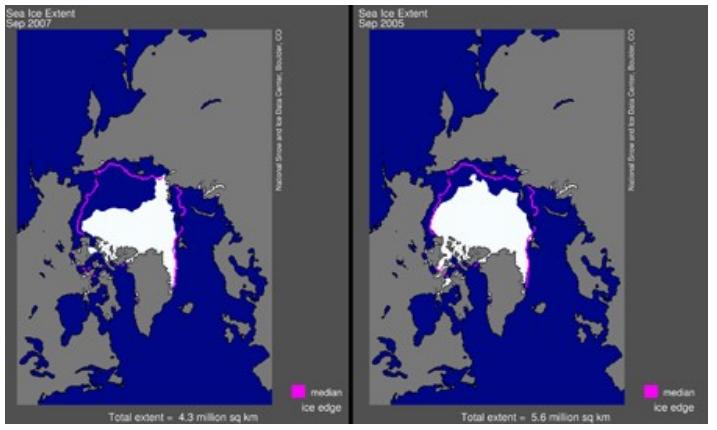
题目:数学与气候变化_融化的北极 介绍:北极的冰面覆盖状况正处于危险境地。由于全球气候变暖,夏天的海洋冰面覆盖面积正以每年约70,000平方公里(苏格兰国家的面积)的速度消失。关于永久冰层是否会从北极圈消失以及什么时候消失的猜想有很多,只有少数模型推测会多于100年,更多的预测是北极圈的冰川会在我们有生之年完全融化。 |
|
题目:蝴蝶效应 介绍:美国数学家、气象学家、“混沌理论之父”洛伦兹在马萨诸塞州理工学院当教授时,发现了“一个系统某部分的微小变化可能导致另一部分的巨大变化”这一现象。蝴蝶效应理论的第一次出现,是在他1972年发表的论文《可预测性报告:一只蝴蝶在巴西拍一下翅膀会不会在德克萨斯州引起一场龙卷风?》中。 |
|
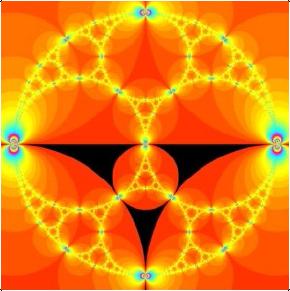
题目:非欧几何与因陀罗珍珠 介绍:许多人会对右图所示的分形之美和复杂性感到惊奇,该分形称为阿波罗垫,是由相切的圆非常复杂地排列。然而很少有人知道象这样的分形与双曲空间的拼接密切相关,在这里我们将探索在这些拼接背后的数学以及它们如何产生漂亮的分形图象。在双曲空间中,距离不是按通常的方式来测量,在双曲测度下,两点间的最短距离不再是沿直线,而是沿不同类型的曲线。 |
|
题目:固有频率与音乐 介绍:如果敲击一个物体,你会听到声音,这是因为达到了物体的固有频率使它振动,这与物体的形状和材质有关。用指关节敲打桌子,然后再轻拍一本书,会发现材质越软,发出声音的频率越低(这两种声音均迅速消失,因为纸和木头的阻尼作用)。乐器就是根据这种现象,采用合适的材料和形状来产生悦耳的声音,并最终形成旋律。 |
|
题目:矩阵模拟世界之_粒子模型 介绍:建模是许多科学和工程领域研究的核心。从本质上讲,模型是一个为了理解复杂系统的行为而以不同方式被简化的。在现代社会,越来越多的模型是由可以高速计算数学模型的计算机来完成的。虽然用计算机模型来模拟的超音速机翼周围的气流流动是极其复杂的,但它却是建立在最基础的程序设计与模拟的原则之上。如何模拟鸟的行为,鱼的行为? |
|
题目:矩阵模拟世界之_元胞自动机 介绍:在矩阵模拟世界的粒子模型中,我们看到可以构建简单的数学模型来研究一切事物包括从鸟的结队飞行到整个星系的碰撞.在这些例子中,一个矩阵可以很方便的被用来存储模拟中所有对象的信息,因此它可以在每个时间步被更新以作为模拟的进展.矩阵或数组不仅仅是在模拟的过程中存储信息的方式,而实际上是模拟的本身. |
|
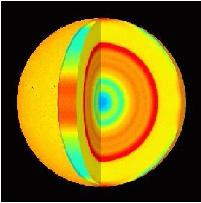
题目:太阳活动 介绍:地质学是通过测量地表振动来研究地震。太阳地质学是太阳物理学中相对比较新的领域,不同的是这里是观测太阳表面的振动,这些振动由太阳内部的驻波形成。在太阳中,我们发现了三维驻波。右图是SOHO卫星上的迈可森多普勒绘图仪观察得到的。这可以表明太阳内部预测的和计算的声波速度间的差别。在红色层,声音比理论预测的传播得更快。蓝色代表声音比预测的速度慢。 |
|
题目:绝不仅仅是方块:从幻方到数独 介绍:古代中国有一个传说。大约三千年前,中国发生了大洪水。为了平息河神的暴怒,人们向洛河做祭祀,但是河神并没平息下来。每次祭河的时候,都有一只乌龟从河里出来。一天,一个男孩注意到乌龟背上的标记,这些标记似乎表示的是数字1到9。这些数字按每一条连线上的和都等于15的方式来排列。人们因此明白了他们祭河的次数不对。乌龟背上的那些标记实际上就是一个幻方。 |
|
题目:量子几何 介绍:在过去的100年左右,物理一直在逐步瓦解我们对空间的直观感受。物理学家告诉我们,空间实际上是一部分弯曲的时空,至少由四个或更高维度组成,而不是由三维所组成。宇宙学家对宇宙的精确几何仍不确定,他们正提出各种奇怪的模型,甚至认为它可能是有穷的。在所有这些思想中,有一种可能是最颠覆直觉的:空间。当你将之放大到一定程度,它将不再是一个光滑且连续的整体。 |
|
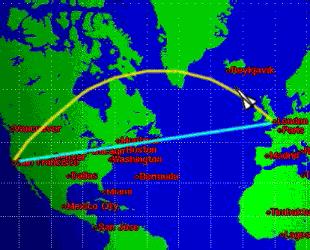
题目:时间和运动 介绍:自开天辟地以来, 人类一直在寻找从A地到B地的更快交通方式。从轮子,到马匹和其他的动物,再到蒸汽机、飞机。现在,最快的交通方式是航天器,如美国宇航局的航天飞机。然而速度并不是行程中的唯一考量,确保选择最短的路线也同样重要。想象你将驾驶着协和式飞机从伦敦到旧金山,那么你不得不在地图上选择一条路线。你会选择以蓝线标记的直线,还是黄线标记的曲线呢? |
|
题目:电话网络中的呼叫路由 介绍:当今社会,我们会觉得英国人打电话到澳洲,或印度人浏览加拿大的计算机上的网页是很寻常的。几乎每个家庭都有自己的电话线,可以连接到城镇中的交换机,再连接到最近城市的主交换机,并从那里连接到世界上任何国家的任何城市。为了使这些庞大而复杂的网络能正常工作,必须用数学和计算机模拟来理解网络。如何设计并控制大型网络以提供可靠的通信系统和有效利用资源? |
|
题目:网络消息 介绍:一组美国研究人员为解决“为什么富庶且受欢迎的人往往会变得更富有,更受欢迎;为什么无人访问的网站永远冷清”而提出了一个数学模型。这个新的研究属于网络理论领域。它还解决了在这一领域长期争论不休的哲学问题。网络在我们的世界无处不在。有社会网络,信息网络和生物网络。不管是哪一种网络,从数学上讲,他们都归结为同一件事:由数学家所称的边所连接的节点集合。 |
|
题目:自相似节拍:斐波那契、L系统、五行打油诗、繁音拍子 介绍:仅仅才出现了一百多年,五行打油诗的魅力就使它成为了世界最流行的诗歌形式。它稍有点不对称的形式,使得它独具魅力,给人以浑然天成之感。1899年随着斯科特乔普林的《枫树叶》一曲的发行,繁音拍子从此风靡全球。这是一种西方音乐传统结合非洲、拉丁的节拍混合而成的产物。它们之所以具有独特的感觉,对称性就是核心因素。它们都有自相似性,这和分形理论有某种联系。 |
|
题目:数学与建筑设计 介绍:过去,建筑对几何学有较多贡献,人们建造房屋,需要测量土地, 这使他们要去研究形状.但在古埃及的巨型金字塔建造4500年之后的今天,数学家们能为建筑做些什么呢? 现代建筑不仅需要结构合理,还要考虑外观令人愉悦,符合设计规则,服从财政预算,最佳地满足目标,最大化能效.设计过程归结为一个复杂的优化问题.基于湍流的数学模型,借助于计算机可以模拟高层建筑的空气动力学特性. |
|
题目:数的艺术 介绍:数学家和艺术家相互怀疑并非闻所未闻,但在艺术与自然界的许多形体具有数量关系。事实上,许多数学家具有强烈的美学创造力。在英国布里斯托尔的惠普校园,一群研究人员正在一个项目的支持下,走入了先进的数学和美妙的艺术世界里。右图是惠普主大厅展览的西蒙托马斯的超锥雕塑,其“柏拉图式的形式”是由一系列经过旋转后的同心环来表示,环的半径呈指数级下降并且每个环的宽度与它的半径成一定比例。 |
|
题目:重建生物树 介绍:达尔文的进化论彻底改变了人类的思想,从严谨的科学到宗教。遗传学的最新进展给达尔文的基本理念一个全新维度,并赋予它丰富的论据。生物学和数学在他们漫长的发展历程中是相对独立的学科,与这形成鲜明对比的是数学和物理之间的高度交叉融合。但这将会发生变化,当科学家开发出更快的基因和全基因组排序方法时,遗传学正经历着一场信息爆炸。要求数学方法去处理海量数据,并推出真正的基本演化路径。 |
数学与统计学院 College of Mathematics and Statistics
地址:重庆大学虎溪校区理科大楼D栋 邮编:401331